주성분 분석(主成分分析, Principal component analysis; PCA)은 고차원의 데이터를 저차원의 데이터로 변환시키는 기법을 말합니다. 이 때 서로 연관 가능성이 있는 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간(주성분)의 표본으로 변환하기 위해 직교 변환을 사용합니다. 데이터를 한개의 축으로 사상시켰을 때 그 분산이 가장 커지는 축을 첫 번째 주성분, 두 번째로 커지는 축을 두 번째 주성분으로 놓이도록 새로운 좌표계로 데이터를 선형 변환합니다. 이와 같이 표본의 차이를 가장 잘 나타내는 성분들로 분해함으로써 데이터 분석에 여러 가지 이점을 제공합니다. 이 변환은 첫째 주성분이 가장 큰 분산을 가지고, 이후의 주성분들은 이전의 주성분들과 직교한다는 제약 아래에 가장 큰 분산을 갖고 있다는 식으로 정의되어있습니다. 중요한 성분들은 공분산 행렬의 고유 벡터이기 때문에 직교하게 됩니다.
차원의 저주란? (자세한 내용은 여기를 참고)
하나의 변수는 하나의 차원을 의미하는데, 차원이 증가할 수록 데이터가 표현해야 하는 공간은 복잡해집니다.
차원이 커질수록 해를 구하기 위한 방정식이 늘어나고 그에 따라 sample 수가 충분하지 못하면 해 공간이 불안정해집니다. (이는 회귀로 보자면 계수의 신뢰 구간이 넓어지는 것으로 말할 수 있습니다)
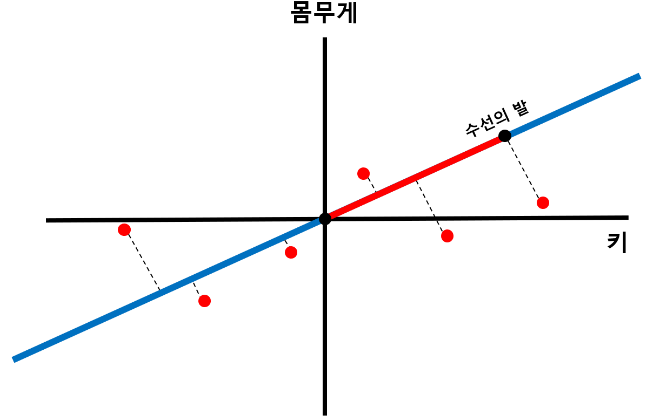
2차원 데이터를 1차원으로 낮춰보았습니다.