[5.1 회귀 소개]

회귀 분석: 데이터 값이 평균과 같은 일정한 값으로 돌아가려는 경향을 이용한 통계학 기법

회귀: 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법

머신러닝 회귀 예측의 핵심 -> 주어친 피처와 결정 값 데이터 기반에서 최적의 회귀 계수를 찾아내는 것

• 회귀 계수: 선형, 비선형 회귀 구분
• 독립변수의 갯수: 단일회귀, 다중 회귀

선형회귀: 실제값과 예측값의 차이를 최소화하는 직선형 회귀선을 최적화하는 방식

[5.2단순 선형 회귀를 통한 회귀 이해]

• 단순 선형 회귀: 독립변수 하나, 종속변수 하나인 선형 회귀
• 회귀 계수를 선형으로 결합하는 회귀 함수를 구해 여기에 독립변수를 입력해 결괏값을 예측함

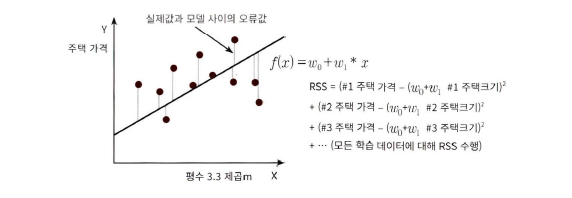
• 잔차: 실제 값과 회귀 모델의 차이에 따른 오류 값
• 최적의 회귀 모델 -> 잔차 합이 최소가 되는 모델 = 오류 값 합이 최소가 될 수 있는 최적의 회귀 계수 찾기
• Errors^2 = RSS를 최소로 하는 w0, w1, 즉 회귀 계수를 학습을 통해 찾는 것이 머신러닝 회귀의 핵심
• RSS = 비용함수 = 손실 함수

[5.3 비용 최소화하기 - 경사 하강법 소개]

• 경사 하강법: 점진적으로 반복적인 계산을 통해 W파라미터 값을 업데이트하면서 오류 값이 최소가 되는 W 피라미터를 구하는 방식 -> w0(작으면 좋음), w1(작으면 좋음), 예측오차(크면 좋음) 도출됨