[6.1 차원축소 개요]

• 차원축소: 다차원 데이터 세트의 차원을 축소해 새로운 차원의 데이터 세트를 생성

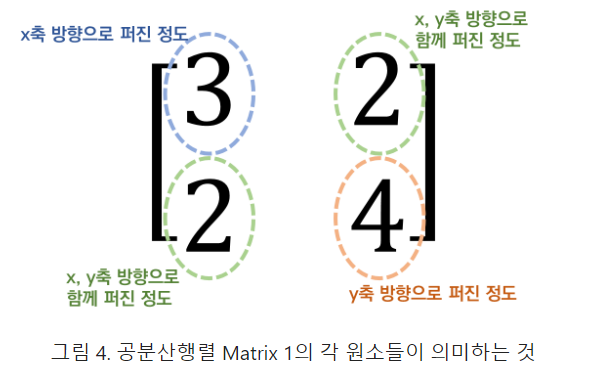
• 차원이 커질수록 -> 데이터 포인트 거리 멀어져서 희소한 구조, 피처간에 상관관계가 높아져 다중공선성 문제 발생

• 차원 축소하면 -> 직관적으로 데이터 해석 가능, 학습에 필요한 처리 능력 줄일 수 있음

• 차원 축소를 통해 데이터를 잘 설명할 수 있는 잠재적인 요소를 추출!!!

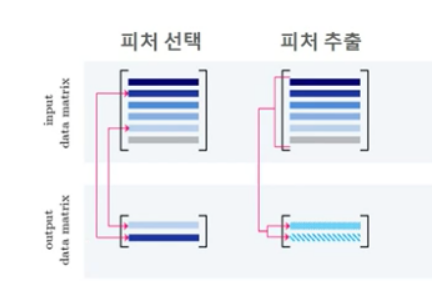
• 피처 선택: 특정 피처에 종속성이 강한 불필요한 피처는 아예 제거, 데이터의 특징을 잘 나타내는 주요 피처만 선택

• 피처 추출: 피처를 함축적으로 더 잘 설명할 수 있는 또 다른 공간으로 매핑해 추출

[6.2 PCA]

PCA: 여러 변수 간에 존재하는 상관관계를 이용해 이를 대표하는 주성분을 추출해 차원을 축소하는 기법, 가장 높은 분산을 가지는(입력 데이터의 변동성이 큰) 데이터의 축을 찾아 이 축으로 차원을 축소, 입력 데이터 세트를 저차원 공간에 투영해 차원을 축소하는 기법

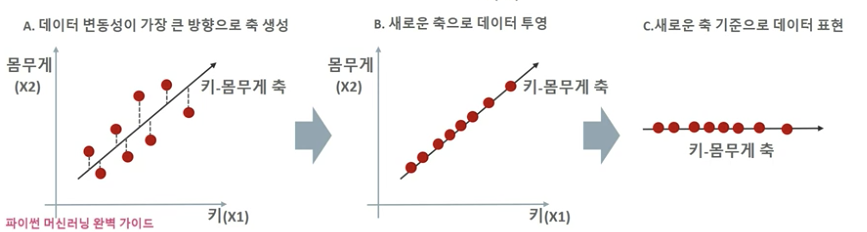
2차원 -> 1차원

• 가장 큰 데이터 변동성을 기반으로 첫 번째 벡터 축 생성, 두번째는 이 벡터 축에 직각이 되는 벡터를 축으로, 세 번째는 두 번째 축과 직각이 되는 벡터 설정 -> 이런식으로 벡터 축의 개수만큼의 차원으로 원본 데이터 차원 축소

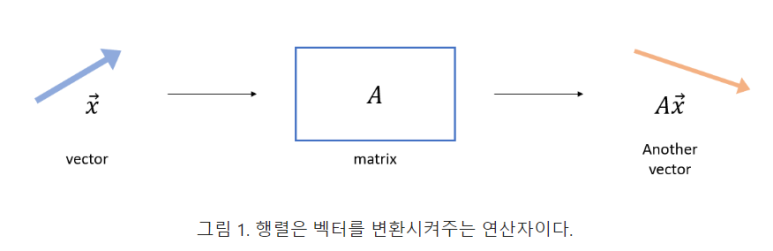
• 선형변환: 특정 벡터에 행렬 A를 곱해 새로운 벡터로 변환하는 것

• 행렬은 선형 변환 연산이다.